Für diesen Trick nutzt ihr am besten einen Taschenrechner. Dann denkt ihr euch eine Zahl aus, die aus drei Ziffern besteht, die immer kleiner werden. Also zum Beispiel 742 oder 983 oder 421. Nehmen wir hier als Beispiel einfach mal die Zahl 983. Das tippt ihr nun in euren Taschenrechner. Jetzt drückt ihr die Minus-Taste und zieht die Zahl von eurer ausgedachten in umgekehrter Reihenfolge wieder ab. Also: 983 – 389. Das ergibt: 594. Dieses Ergebnis merkt ihr euch. Jetzt drückt ihr die Plus-Taste. Gebt nun wiederum die umgekehrte Zahlenfolge ein: 594 + 495. Das Ergebnis ist 1.089. Soweit so gut. Das faszinierende ist: Das Ergebnis ist IMMER 1.089, egal welche Zahlenfolge ihr zu Beginn gewählt habt. Glaubt ihr nicht? Ist aber so! Wir zeigen euch noch ein Beispiel: 421. Der Rechenweg ist:

421 – 124 = 297
297 + 792 = 1.089
Probiert es aus! Und dann könnt ihr auch einfach andere verblüffen. Stellt ihnen die Aufgabe und sagt ihnen schon vorher das Ergebnis. Sie werden staunen…
Aber warum kommt immer dasselbe Ergebnis raus?
Dafür gibt eine mathematische Gleichung. Wem das zu kompliziert ist, der kommt einfach in ein paar Jahren noch mal auf unsere Seite. Es setzt ein gewisses mathematisches Grundverständnis voraus. Und wer das noch nicht hat, der genießt einfach den coolen Trick – der funktioniert nämlich auch, ohne dass man den Rechenweg dahinter verstehen muss.

Für die Geübteren: Man kann Zahlen in z.B. Hunderter, Zehner und Einer aufteilen. Wenn man das, tut ergibt sich aus der Zahl 983: 100 x 9 + 10 x 8 + 3 x 1. Und nun stellen wir uns vor, dass für je Hunderter, Zehner und Einer einfach aus der Zahl ein Buchstabe wird. Für die Hunderter ‚a‘ (im Falle unseres Beispiels ist ‚a‘ = 9) für die Zehner ‚b‘ (bei uns ist ‚b‘ = 8) und für die Einer ‚c‘ (in unserem Beispiel ist ‚c‘ = 3). Daraus ergibt sich als mathematische Gleichung 100a+10b+1c. Möchten wir die Zahl umdrehen, vertauschen wir die Buchstaben: 100c+10b+1a. Der erste Rechenweg für 983 – 389 würde also als generelle mathematische Gleichung lauten:
100a+10b+1c – (100c+10b+1a)
Löst man hier die Klammer auf, vertauschen sich die Vorzeichen, die vorher in der Klammer standen:
100a+10b+1c-100c-10b-1a
+10b -10b‘ hebt sich gegenseitig auf, so dass übrig bleibt:
100a+1c-100c-1a
Auch das kann man noch weiter vereinfachen, bis am Ende da steht:
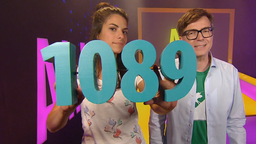
100(a-c) + 1(c-a)
= 100(a-c) +1(-a+c)
= 100(a-c) -1(a-c)
= 99(a-c)
Daraus ergibt sich, dass das Ergebnis immer ein Vielfaches von 99 ist (Hier listen wir die mal alle auf: 2X99=198, 3x99=297, 4x99=396, 5X99= 495, 6x99=594, 7x99=693, 8x99=792, 9x99=891). Und das besondere an diesen Vielfachen ist, dass sie umgedreht addiert (also 198+891, etc.) 1089 ergeben. Immer! Bei allen! Mathe ist so faszinierend…