
Was war am 21. April 2001? Da lief „Wissen macht Ah!“ zum allerersten Mal im Fernsehen. Und was war das für ein Wochentag? Es war ein Samstag! Gut – wir wussten das jetzt. Aber mit ein bisschen Mathematik und ein paar Infos, die wir euch hier geben, könnt ihr zu jedem x-beliebigen Datum den Wochentag ermitteln.
Und so funktioniert's:
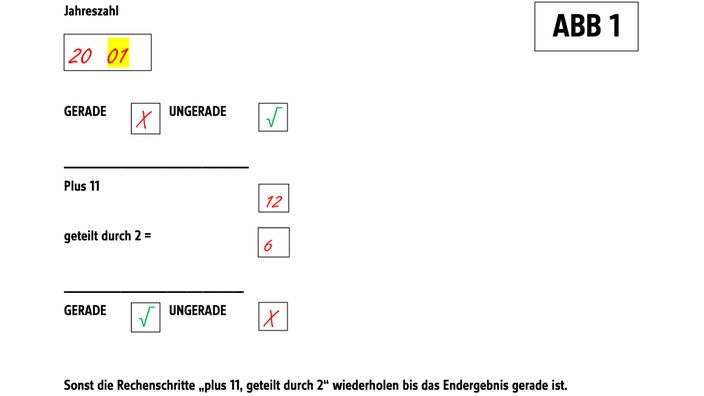
Klickt euch durch die Anleitung!
Galerie
Galerie
Galerie
Galerie
Galerie
Galerie
Galerie
Und? An welchem Wochentag seid ihr geboren worden? Schreibt in unser Gästebuch!









31 Kommentare
Kommentar 31: ABC schreibt am 28.05.2022, 13:07 Uhr :
Dienstag😉. Schlau :)
Kommentar 30: MaZi schreibt am 29.12.2021, 21:12 Uhr :
Gibt es einen Ankertag im Januar? Wenn nicht, wir rechnet man das dann?
Kommentar 29: Blahblah schreibt am 09.08.2021, 19:41 Uhr :
SAMSTAG GEIL DANKE VIELMALS :)
Kommentar 28: Ahtene:) schreibt am 05.08.2021, 18:27 Uhr :
Ich komme in mathe relativ gut mit, aber die quatratur des kreises ist mir einfach zu hoch. Könnt ihr mir das erklähren ihr macht das ziemlich gut. Danke.
Kommentar 27: Lizi schreibt am 21.06.2021, 12:52 Uhr :
Bei mir klappt es nicht!
Kommentar 26: Lizi schreibt am 21.06.2021, 12:49 Uhr :
Ich bekomme den Falsche Tag heraus.
Kommentar 25: Anonym schreibt am 06.04.2021, 11:13 Uhr :
Total schlau!!!!!!!!!!!
Kommentar 24: TATA schreibt am 13.10.2020, 18:42 Uhr :
Ziemlich komplizirtg
Kommentar 23: Stefan schreibt am 07.06.2020, 14:10 Uhr :
Hallo liebe WissenmachtAh-Redaktion, die erste Seite des Algorithmus ist leider nicht eindeutig formuliert. Was genau muss man hier in Welchem Fall machen? Vielleicht könnt ihr das noch einmal präzisieren, damit niemand frustriert ist? Beispiel 6.6.2020: 20 ist gerade, also keine +11. Wenn man nun nicht durch 2 teilt erhält man ein falsches Ergebnis, nämlich Mittwoch. Wenn man durch 2 teilt, ist es korrekt, nämlich Samstag. Vielleicht ist das der Fehler mancher andere Kommentarschreiber. vielen Dank für eure schönen Sendungen und viele Grüße
Kommentar 22: Johan schreibt am 05.06.2020, 21:15 Uhr :
Wir haben uns wohl verrechnet, jedenfalls kamen immer falsche Ergebnisse raus. An vielen Stellen war der Rechenweg nicht klar... mehr Beispiele wären super!
Kommentar 21: Vera schreibt am 31.05.2020, 15:19 Uhr :
Warum erzählt man das denn.