Unser Gehirn versucht, in vorhandene Formen etwas hinein zu interpretieren, um uns die Wahrnehmung der Welt zu erleichtern. Dabei misst das Gehirn das, was es wahrnimmt, an dem, was es bereits kennt. Um an das Bekannte möglichst nah heranzukommen, ergänzt das Gehirn manchmal sogar einfach Fehlendes. Ein gutes Beispiel hierfür ist das Kanizsa-Dreieck (ABB 1). Es ist nach dem italienischen Psychologen Gaetano Kanizsa benannt, der sich damit beschäftigt hat, wie wir die Welt wahrnehmen.

Das erstaunliche beim Kanizsa-Dreieck ist, dass es gar kein Dreieck gibt. Es gibt nur drei Kreise, bei denen jeweils eine Ecke fehlt. Da das Gehirn aber immer nach bekannten Formen sucht, sehen wir nicht drei unvollständige lila Kreise - die zwar da sind, die unser Gehirn als Form aber nicht wiedererkennt - , sondern ein nicht vorhandenes weißes Dreieck - das uns als Form bereits bekannt ist.
Das Gehirn versucht immer aus den Daten, die es von den Augen empfängt ein räumliches Bild zusammenzusetzen. Klar - wir leben ja in einer räumlichen Welt. Das drückt sich zum Beispiel darin aus, dass Menschen, die auf uns zukommen, in der Ferne klein aussehen und beim Näherkommen immer größer werden. Aber wir wissen: der Mensch ist immer gleich groß! Nur das räumliche Sehen sorgt dafür, dass die Größenunterschiede entstehen.
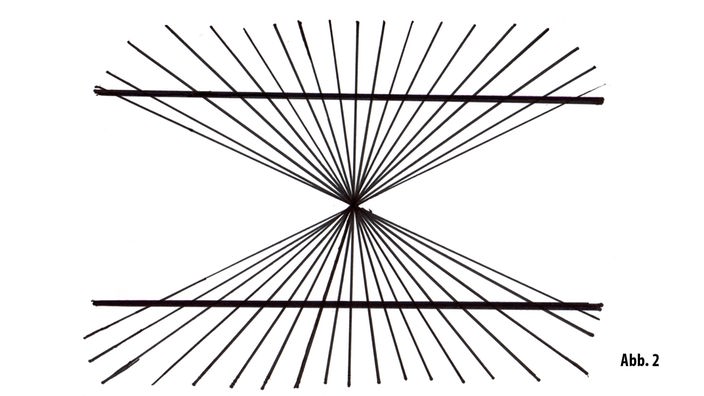
Interessant ist auch die Heringsche Täuschung (ABB 2). Auch der deutsche Wissenschaftler Ewald Hering hat sich mit der menschlichen Wahrnehmung beschäftigt und als erster diese Täuschung gezeigt. Man sieht ganz viele Linien, die sich in einem Mittelpunkt kreuzen und zwei Linien, die waagerecht verlaufen. Sind diese waagerechten Linien gerade oder gebogen? Schaut genau hin! Sie sind gerade!
Aber warum denken wir, sie seien gebogen? Das hat mit den Winkeln zu tun, die an den Stellen entstehen, wo sich die waagerechte Linie und die anderen kreuzen. Unser Gehirn hat eine Vorliebe für 90-Grad-Winkel, also für rechte Winkel. Stumpfe Winkel, also solche, die größer sind als 90 Grad, nehmen wir etwas kleiner wahr, um sie den vom Gehirn bevorzugten rechten Winkeln anzunähern.
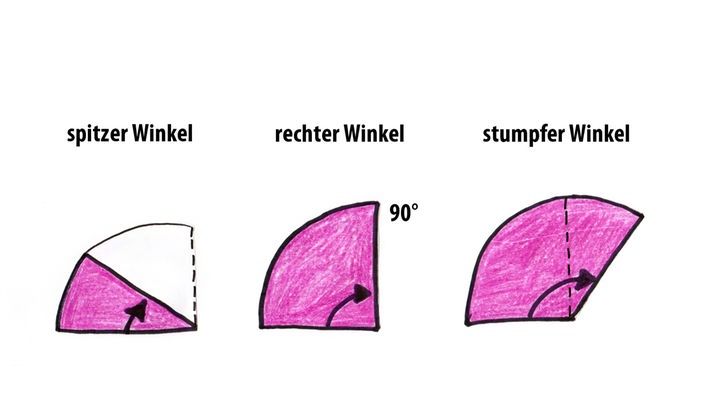
Spitze Winkel, also solche, die kleiner sind als 90 Grad, nehmen wir aus dem gleichen Grund etwas größer wahr.
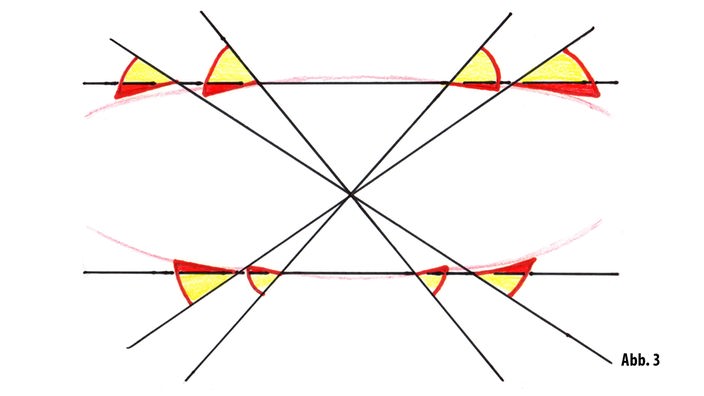
Bei der Heringschen Täuschung entstehen eine ganze Reihe spitzer Winkel, die das Gehirn automatisch vergrößert. Was dann passiert kann man auf ABB 3 gut sehen: die roten Bereiche zeigen das, was das Gehirn dazurechnet. Und aus diesen vielen kleinen ein bisschen falschen Winkelinformationen errechnet das Gehirn eine gebogene (rote) Line - obwohl sie eigentlich schnurgerade ist.
Ah!