Man kann alle möglichen Dinge errechnen. Man kann sogar herausfinden, wie groß die Wahrscheinlichkeit ist, dass eine bestimmt Sache eintrifft oder nicht. Also ist sogar der Zufall berechenbar. Dabei teilt man die verschiedenen Möglichkeiten in Mengen ein. Ein konkretes Beispiel ist:
Das Ziegen-Problem

Der Kandidat einer Quizshow steht vor drei geschlossenen Toren (Tor A, Tor B, Tor C). Hinter einem der Tore ist der Hauptpreis. Hinter den zwei anderen Toren befindet sich je eine Ziege. Der Kandidat soll sich für eins der Tore entscheiden. Was auch immer dahinter ist, der Kandidat darf es behalten. Natürlich ist ihm daran gelegen, den Hauptgewinn einzusacken. Er entscheidet sich für Tor A. Der Moderator öffnet jetzt Tor B. Dahinter steht eine Ziege. Jetzt darf sich der Kandidat noch mal umentscheiden. Soll er bei seiner ersten Wahl - Tor A - bleiben, oder soll er sich für Tor C entscheiden?
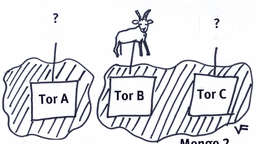
Tatsächlich hat der Kandidat höhere Chancen auf den Hauptgewinn, wenn er sich noch einmal umentscheidet. Die Chance ist sogar doppelt so hoch, wenn er sich für Tor C entscheidet. Aber warum ist das so? Ganz spontan würde man doch denken, die Chancen stehen fifty-fifty?
Entscheidet sich der Kandidat das erste Mal, ist die Wahrscheinlichkeit, direkt den Hauptgewinn zu wählen 1 zu 2. Das heißt eine Gewinnchance zu drei Wahlmöglichkeiten oder Toren. Jetzt werden die drei Tore in zwei Mengen unterteilt:

Menge 1: das gewählte Tor A und der Gewinnchance ein Drittel
Menge 2: die beiden anderen Tore B und C mit der Gewinnchance zwei Drittel
Der Moderator zeigt jetzt aus Menge 2 eine Niete: Tor B. Damit hat Menge 2 immer noch die Gewinnchance zwei Drittel aber nur noch eine Wahlmöglichkeit. Somit hat diese - nämlich Tor C - jetzt die komplette Gewinnchance von zwei Dritteln. Tor A aus der Menge 1 hat weiterhin nur die Gewinnchance von einem Drittel.
Wer sich noch einmal umentscheidet, verdoppelt also seine Gewinnchancen: Zwei Drittel zu einem Drittel!